مدلسازی یکی از تکنیکها در ارزیابی کارایی سیستم است. زمانی که ایدهای که در قالب یک سیستم میخواهیم آن را ارزیابی کنیم به قدری نو باشد که هنوز حتی سیستمهای شبیهسازی مناسبی نیز برایش وجود نداشته باشد، تکنیک مدلسازی و روشهای آمار و احتمالات در ارزیابی کارایی سیستم به کمک ما خواهد آمد.
مقدمهای برای یادآوری آمار و احتمالات مهندسی
فضای نمونه یا مجموعه مرجع: در نظریه احتمال فضای نمونه یا فضای نمونهای (به انگلیسی: Sample space) مجموعه تمام نتایج ممکن (حالات) از یک آزمایش تصادفی (پدیده تصادفی) است که آن را با نماد S، Ω یا U (مخفف universe به معنی جهان) نشان میدهند. به عنوان مثال، برای آزمایش پرتاب سکه، فضای نمونه برابر است با مجموعه {شیر، خط} و برای یک تاس شش وجهی، فضای نمونه برابر است با مجموعه {۱، ۲، ۳، ۴، ۵، ۶}.
رخداد یا Event: مجموعه تمام حالتهای یک رخداد (مانند مجموعه یا فضای حالتهای عدد زوج یک تاس) است و زیر مجموعه فضای نمونه یا مجموعه مرجع است.
مجموعههای زیر مجموعه فضای نمونه میتوانند با هم یکسری اجتماعات و اشتراکات یا متمم یک مجموعه با عنوان جبر مجموعهها داشته باشند.
پیشامد مستقل (disjoint – mutually exclusive): اگر P(A) و P(B) دو پیشامد باشد که اشتراکشان صفر باشد، دو پیشامد مستقل مینامیم.
در این حالت و از آنجایی که P(A Ո B) برابر صفر است اجتمال دو پیشامد حاصل جمع آنها است P(A U B)=P(A)+P(B).
احتمال وقوع یک رخداد برابر است با تمام حالتهای این رخداد به تمام حالتها.
P(S) = 1
P(A U B) = P(A) + P(B) – P(A Ո B)
احتمال شرطی (conditional): فرض کنید دو پیشامد A و B در فضای نمونهای یکسان داده شدهاند در حالی که P(B) > 0 احتمالی شرطی A در حالی که B رخ داده باشد یا .به عبارت دیگر، احتمال شرطی زمانی است که احتمال وقوع یک پیشامد را به یک پیشامد دیگر منوط کنیم. احتمال وقوع پیشامد A به شرط اینکه پیشامد B رخداد باشد. احتمال A آنگاه B.
![]()
که در آن P(B) > 0 است.
اصل ضرب: برای احتمال اشتراک دو پیشامد A و B میتوان نوشت: P(A Ո B) = P(A | B) P(B)
قاعده کلی ضرب به این صورت است که
![]()
احتمال اشتراک (احتمال شرطی – conditional probability)
در مبحث احتمال، وقوع یا عدم وقوع یک پیشامد (پدیده تصادفی) میتواند در رخداد پیشامدهای دیگر تاثیرگذار باشد. برای مثال، ممکن است ابری بودن آسمان، احتمال بارندگی در صبح فردا را افزایش دهد. در چنین حالتی بحث احتمال شرطی (Conditional Probability) بوجود میآید. احتمال وقوع A به شرط اینکه B رخ دهد برابر است با P(A|B) که در آن P(B) > 0.
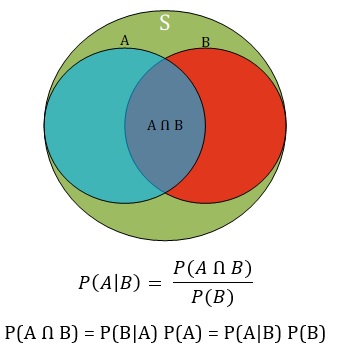
میدانیم احتمال وقوع هر پیشامد (پدیده تصادفی) برابر است با نسبت اعضای آن پیشامد به تعداد اعضای فضای نمونه. در احتمال شرطی، احتمال وقوع پیشامد A به شرط اینکه پیشامد B رخ داده باشد، فضای نمونه به B کاهش پیدا میکند. اعضای پیشامد A نیز به اعضایی که در اشتراک با فضای نمونه B است کاهش مییابد.
به عنوان مثال، اگر فضای نمونه و مجموعه A و B به صورت زیر باشد:
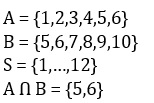
آنگاه:
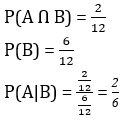
احتمال وقوع پیشامد A در صورتیکه پیشامد B اتفاق افتاده باشد از فضای نمونه مشخص شده قابل محاسبه است و برابر است با قانون احتمال اشتراکی.
حال اگر A و B از یکدیگر مستقل باشند، میتوان گفت که P(A Ո B) = P(A) P(B) و P(A U B) = P(A) + P(B). در این حالت احتمال شرطی معادل P(A | B) = P(A) میشود. به عبارت دیگر احتمال وقوع B بروی احتمال وقوع A تاثیری ندارد. به این حالت قانون ضرب احتمالات نیز گفته میشود.
حال اگر تعداد احتمالات از دو حالت بیشتر باشد و تمامی آنها دو به دو از همدیگر مستقل باشند،
P(A1,A2,…,An) = P(A1) P(A2) … P(An)
احتمال متمم یک پیشامد برابر احتمال کل منهای احتمال اصل پیشامد است. P(Ā) = 1 – P(A)
و اگر تمامی پیشامدها دو به دو از همدیگر مستقل باشند، احتمال اشتراک متممها نیز برابر با حاصل ضرب متممها
P(Ā1 Ո Ā2 Ո … Ān) = P(Ā1) P(Ā2) … P(Ān)
سیستمهای سری و موازی – Series-Parallel Systems
انواع متریک که از سه جنس مختلف هستند شامل سرعت، دقت و قابلیت دسترسی بود. در متریک از جنس سرعت عنوان میشود، یک سیستم چقدر سریع کار میکند. در متریک از جنس دقت عنوان میشود یک سیستم چقدر دقیق کار میکند و در متریک از نوع قابلیت دسترسی عنوان میشود یک سیستم چه مقدار قابل دسترسی است.
اگر بخواهیم متریک قابلیت اطمینان سیستمها را با استفاده از تکنیک مدلسازی ارزیابی کنیم، میتوان تمام سیستمها را حالتهایی از اجزا سری و موازی متصل به هم هستند. اگر قابلیت اطمینان هر جزء را داشته باشیم، در نهایت میتوانیم از طریق قوانین آماری قابلیت اطمینان کل سیستم را مدلسازی کنیم.
در نظر داشته باشید برای مدلسازی یک سیستم در ابتدا از مفروضات ساده مانند مستقل بودن قابلیت اطمینان اجزا یک سیستم از یکدیگر استفاده میکنیم. پس از آن شرایط را تغییر میدهیم. در ریاضیات نیز تلاش بر سادهسازی حداکثری معادلات پیچیده است.
سیستمهای سری – Series Systems
فرض کنید یک سیستم یا جزئی از یک سیستم (subsystem) را داریم (مانند یک باکس است و از داخل آن خبر نداریم). سیستم مشخص شده دارای قابلیت اطمینان Ri است که عددی بین 0 و 1 است. به عبارت دیگر میتوان گفت سیستم یا جزء سیستمی Ri با یک احتمالی یا کار میکند (1) یا کار نمیکند (2).
![]()
چند سیستم از حالت تعریف شده بالا به صورت سری به یکدیگر متصلند.

اگر بخواهیم سیستمی مانند نمونه بالا که اجزا (CPU، NIC، HDD و …) آن به صورت سری به همدیگر متصل هستند و احتمال قابلیت اطمینان کارکرد هر کدام از دیگری مستقل است (independent components) را مدل کنیم قابلیت اطمینان از کارکرد صحیح سیستم S برابر میشود با احتمال کارکرد سیستم S. زمانی سیستم S کار میکند که تمام اجزا یا زیر سیستمهایش درست کار کنند. به عبارت دیگر زمانی سیستم S درست کار میکند که زیر سیستمهای A1 و A2 تا An درست کار کنند.
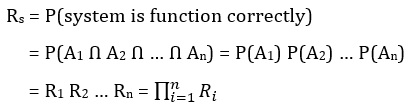
این قانون ساده بدست آمده در مورد قابلیت اطمینان یا احتمال کارکرد صحیح یک سیستم سری با اجزا مستقل برای تمام سیستمهای سری با اجزای مستقل قابل پیادهسازی است.
برای مدل کردن دسترسیپذیری یا availability یک سیستم میتوان از مفروضات مستقل بودن اجزا و حاصل ضرب احتمال دسترسیپذیری آنها استفاده کرد. فرمول دسترسی پذیری یک سیستم از دو متغییر به نامهای MTTF (زمان ایجاد خطا – Mean Time To Failure) و MTTR (زمان برطرف کردن خطا – Mean Time To Repair) بدست میآید.
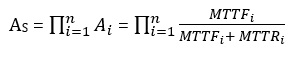
سیستمهای موازی – Parallel Systems
در این سیستمها نیز همانند سیستمهای سری برای مفروضات اولیه و سادهسازی مدلسازی سیستم را شامل چند جزء موازی در نظر میگیریم که هر کدام از این اجزا دو به دو مستقل از هم هستند.
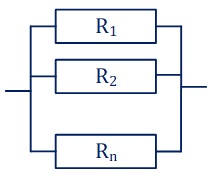
اگر Ei برابر با جزء i باشد، Ep سیستمی است که از n جزء موازی تشکیل شده است. در این حالت میگوییم احتمال کارکرد صحیح سیستم برابر است با P(Ep) یا همان Rp.
Rp = P(Ep)
در سیستمهای موازی در صورتیکه حتی یکی از زیر سیستمها کار کند و FAIL نشده باشد سیستم کار میکند. زمانی سیستم به مشکل برخورد کرده یا FAIL میشود که تمام اجزا FAIL شوند. با این تعریف، برای محاسبه احتمال FAIL شدن یک سیستم موازی باید احتمال Ēp بدست آید.
P(ĒP) = P(Ē1 Ո Ē2 Ո … Ո Ēn)
= P(Ē1) P(Ē2) … P(Ēn)
احتمال وقوع متمم یک رخداد برابر است با کل فضای نمونه منهای اصل رخداد. P(Ēi) = 1 – P(Ei)
با توجه به موارد فوق و قانون حاصل ضرب احتمال رخدادهای مستقل، احتمال کارکرد صحیح یک سیستم موازی برابر است حالت زیر
![]()
از همین روش و مقادیر MTTN و MTTR در جایی که Ai برابر است با
![]()
میتوان میزان دسترسیپذیری را در سیستمهای موازی بدست آورد.
![]()
سیستمهای ترکیبی سری – موازی
در اکثر موارد اجزا یا زیرسیستمهای یک سیستم کلی فقط سری یا موازی نیستند و به صورت ترکیبی قرار گرفتهاند. فرض کنید یک سیستم VoIP شامل دو کنترل کننده سیگنال موازی و سه عملگر انتقال دیتا voice موازی به صورت سری به همدیگر مانند تصویر زیر متصل شدهاند.
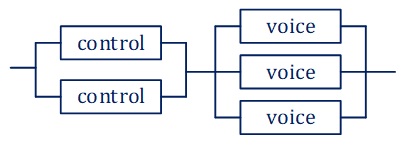
قابلیت اطمینان هر کانال کنترلی با یکدیگر برابر و برابر است با Rc
قابلیت اطمینان هر کانال صدا با یکدیگر برابر و برابر است با Rv
سیستم (با احتمال قابلیت اطمینان کارکرد Rs) تا زمانی که یکی از کانالهای کنترل (با احتمال قابلیت اطمینان کارکرد Rc) و حداقل یکی از کانالهای صدایش (با احتمال قابلیت اطمینان کارکرد Rv) در حال کار کردن باشد کار خواهد کرد. به این ترتیب قابلیت اطمینان سیستم با فرمول زیر محاسبه میشود.
![]()
در نظر داشته باشید در درس ارزیابی کارایی سیستم به دنبال اثبات معادلات ریاضی و آمار نیستیم. فرمولهای آمار ابزاری در فرآیند ارزیابی کارایی است.










