آمار و احتمال در ارزیابی کارایی سیستم – بخش دو

پس از بررسی مقدماتی آمار و احتمال و ارتباط با آن با ارزیابی کارایی سیستم، در این قسمت به مدل‌سازی خطای کانال ارتباطی، قانون‌های دیگری از آمار، روش bridging و درخت خطا می‌پردازیم.

مدل‌سازی خطای کانال ارتباطی

دریافت اشتباه اطلاعات در شیکه‌های کامپیوتری جزء جدا ناپذیری از این مجموعه است. این خطاها در شیکه‌های موبایل نیز بیشتر می‌شود. به همین علت باید بتوانیم با روش‌های مدیریت خطا، خرابی‌های اتفاق افتاده در سطح شبکه را جبران کنیم. در این قسمت می‌خواهیم خطای کانال را مدل‌سازی کنیم.

اگر S فضای نمونه و حالت‌های A و B و (A Ո B) (فضای نمایش داده شده با عدد 2)، (A Ո  ) (فضای نمایش داده شده عدد 1) مشابه تصاویر زیر باشند،

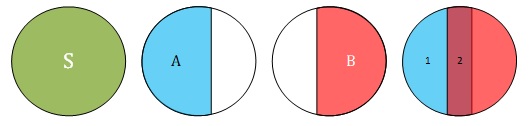
آنگاه

حتی اگر A و B اشتراکی نداشته باشند این قانون صادق خواهد بود چون

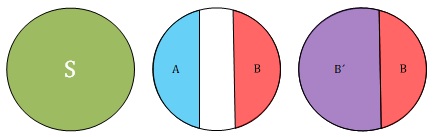
در حالتی که A و B اشتراکی نداشته باشند، احتمال وقوع پیشامد A برابر می‌شود با:

قانون احتمال کل

برای درک این قانون فرض کنید A₁, A₂, … ,A_n پیشامدهایی باشند که فضای نمونه S را تشکیل داده‌اند (پیشامدها اشتراکی با هم ندارند و اجتماعشان فضای نمونه را تشکیل می‌دهد یا به عبارتی افراز کنند) و B یک پیشامد دلخواه باشد.

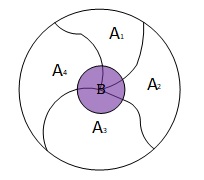
در این صورت بر اساس قانون احتمال کل می‌توان گفت:

مثال: کانال دودویی در یک ارتباط را در نظر بگیرید. کانال در شبکه به معنای لینک یا بستری است که دو نقطه را به هم متصل می‌کند. در این مثال T به معنای ارسال یا transmit و R به معنای دریافت یا receive است. R₀ به معنای دریافت 0، T₀ به معنای ارسال صفر، R₁ به معنای دریافت 1 و T₁ به معنای ارسال 1 است.

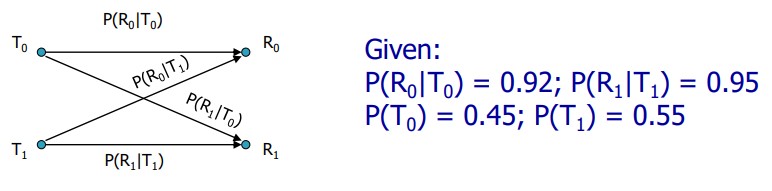
با توجه به این که احتمال ارسال 0 یا 1 اشتراکی با همدیگر ندارد و اجتماعشان کل حالات ارسال را تشکیل می‌دهد، احتمال دریافت 0 یا 1 می‌تواند از قانون ارسال کل محاسبه شود.

اگر احتمال وقتی که ارسال و دریافت 0 باشد 0.92   در نتیجه احتمال دریافت 0 وقتی ارسال 1 بوده برابر است با 0.08

احتمال وقتی که ارسال و دریافت 1 باشد 0.95       در نتیجه احتمال دریافت 1 وقتی ارسال 0 بوده برابر است با 0.05

احتمال ارسال 0، 0.45

احتمال ارسال 1، 0.55 باشد

روش conditioning یا bridging

در برخی موارد، سیستم‌های مدل‌سازی شده را نمی‌توان کاملا به صورت موازی و یا سری در نظر گرفت و این سیستم‌ها مقداری پیچیده‌تر از حالت‌های دیگرند. به عنوان مثال در سیستم تصویر زیر دقیقا نمی‌توان مشخص نمود که چه اجزائی به صورت سری و موازی به همدیگر متصلند.

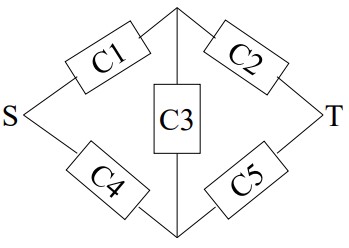
برای ساده کردن سیستم مدل شده بالا، با حذف زیرسیستم C3 می‌توان به یک سیستم ساده‌تر دست یافت. برای حذف زیرسیستم C3 باید تمامی مقادیر ممکن را به آن وارد کنیم و سیستم نتیجه شده را ترسیم کنیم. در نهایت به وضعیتی خواهیم رسید که وضعیت کلی ایجاد شده سیستم به صورت روش‌های قبل قابل حل است.

اگر زیرسیستم C3 قطع باشد، نتیجه سیستم اصلی به صورت تصویر زیر تغییر می‌کند.

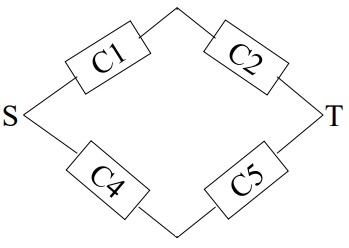
A را Availability در نظر می‌گیریم.

اگر زیر سیستم C3 وصل باشد، نتیجه سیستم اصلی به صورت تصویر زیر تغییر می‌کند.

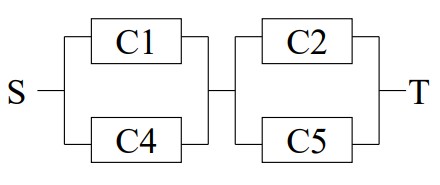
در انتها بایستی Reliability کل سیستم bridge را بدست آوریم. برای اینکار در نظر می‌گیریم با چه احتمالی زیرسیستم C3 می‌تواند up یا down باشد را در مقادیر بدست آمده از Reliability آن حالت‌ها ضرب و دو حالت را به دلیل عدم وجود اشتراک با همدیگر جمع می‌کنیم.

درخت خطا – Fault Tree

در برخی مواقع سیستم را با عناصر مدار منطقی مانند AND، OR، NOT و … مدل می‌کنیم که به آن درخت خطا می‌گوییم. تجزیه و تحلیل درخت خطا می‌تواند برای انجام فرآیند ارزیابی ریسک سیستم مورد استفاده قرار گیرد و هدفش شناسایی علل موثر در خرابی سیستم و کاهش ریسک ها قبل از وقوع است.

فرض کنید یک سیستم کامپیوتری شامل پردازنده، درایو ذخیره‎سازی و کارت شبکه مانند تصویر زیر وجود دارد به صورت‌های سری و موازی به همدیگر متصلند.

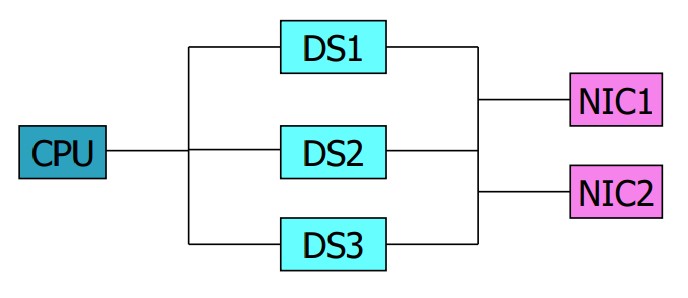
همانطور که گفتیم در روش درخت خطا به دنبال شناسایی عامل موثر در خرابی هستیم. به همین علت مدل‌سازی با عناصر مدار منطقی براساس FAIL شدن سیستم انجام می‌دهیم. برای مدل‌سازی FAIL شدن سیستم باید بگوییم: سیستم زمانی FAIL می‌شود که یا CPU، یا تمامی دیسک‌ها و یا تمامی کارت شبکه‌ها FAIL شود. به این ترتیب مدل مدار منطقی سیستم به صورت زیر تبدیل می‌شود.

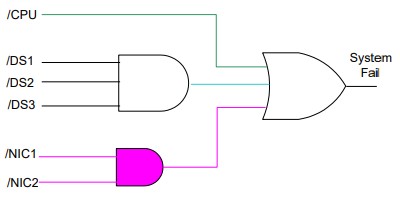
پس از ترسیم مدل‌سازی براساس عناصر مدار منطقی، Reliability سیستم را محاسبه می‌کنیم. Reliability سیستم 1 منهای حالت ترسیم شده درخت خطاست. بنابراین می‌توان نوشت:

آزمایش برنولی – Bernoulli Trail

آزمایش برنولی آزمایشی در آمار و احتمالات است که برآمد آن تصادفی است و یکی از 2 برآمد ممکن موفقیت یا شکست است. این 2 برآمد می‌توان با طرح سوالات بله یا خیر مشخص شود. مانند:

• آیا سکه رو می‌آید؟
• آیا فرزند تازه به دنیا آمده دختر است؟
• آیا این کاندیدا رای می‌آورد؟

بنابراین موفقیت یا شکست عناوینی برای برآمدها هستند و نباید تفسیر شوند. نمونه‌هایی از آزمایش برنولی:

• انداختن سکه که در آن نمونه “رو” بیانگر موفقیت و “پشت” بیانگر شکست است.
• انداختن تاس که در آن عدد 6 برآمد موفقیت و بقیه اعداد شکست است.

فرآیند برنولی عبارتست از انجام مکرر تعدادی آزمایش برنولی مستقل از هم.

آزمایش برنولی در ادامه بیشتر توضیح داده خواهد شد.

متغیرهای تصادفی گسسته – Discrete Random Variable (DRV)

از آنجا که پیشامدها زیر مجموعه‌هایی از فضای نمونه در نظر گرفته می‌شوند، برای محاسبه احتمال آن‌ها باید با محاسبات روی مجموعه‌ها سروکار داشته باشیم، که البته کار ساده‌ای نیست. در عوض می‌توان به کمک تعریف «متغیر تصادفی» (Random Variable)، احتمال بسیاری از پیشامدها را براساس الگوهای احتمالی قابل دسترس، محاسبه کرد زیرا بسیاری از پدیده‌های تصادفی دارای الگوهای مشخصی هستند.

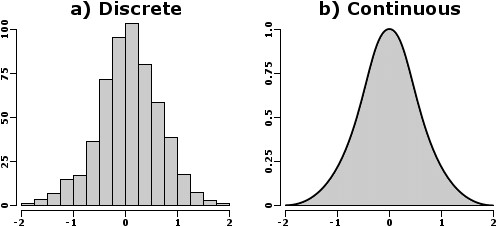
به کمک متغیر تصادفی برای هر پیشامد از فضای نمونه یک عدد از اعداد حقیقی (اعداد صحیح مثبت) در نظر گرفته می‌شود. از آنجایی که پیشامدها به صورت تصادفی رخ می‌دهند، طبیعی است برای هر کدام مقداری تصادفی در نظر بگیریم. به همین علت به چنین متغیرهایی، متغیرهای تصادفی گفته می‌شود. هر چند بعدا متوجه می‌شویم که متغیرهای تصادفی در حقیقت یک تابع هستند نه متغیر!

یک تابع یا mapping ای از فضای نمونه S به مقادیر اعداد حقیقی (فضای نمونه بهینه R) با هدف کاهش حجم فضای نمونه تعریف می‌کنیم. با این کار می‌توانیم فضای نمونه را بهینه کرده و حجم محاسبات را کاهش دهیم.

برای مثال، فرض کنید در پرتاب دو سکه به طور مستقل فضای نمونه به صورت {HH, HT, TH, TT} باشد. اگر متغیر تصادفی X (متغیرهای تصادفی را با حروف بزرگ نمایش می‌دهیم) را تعداد شیرها در نظر بگیریم خواهیم داشت:

X({HT}) = X({TH}) = 1,      X({TT}) = 0,          X({HH}) = 2

از آنجایی که بایستی برای فضای پیشامد تعریف شده که مجموعه‌ای از زیر مجموعه‌های فضای نمونه است احتمال محاسبه شود، می‌توانیم احتمال آن را به صورت زیر بنویسیم:

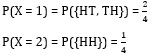
احتمال برای متغیر تصادفی را در حالت‌هایی که پیشامد مجموعه تهی باشد را برابر 0 در نظر می‌گیریم.

استفاده از روابط آمار و ریاضیات در توصیف یک سیستم قابل اثبات است. شاید بتوان نتایج بدست آمده از تکنیک شبیه‌سازی را به چالش کشید، اما به دلیل قابل اثبات بودن ریاضیات، تکنیک مدل‌سازی درگیر این چالش‌ها نخواهد شد.

دلیل دیگر استفاده از مدل‌سازی این است که در برخی موارد مانند شیکه‌های بی‌سیم مانند شیکه‌های موبایل به دلیل ناپیدا بودن بسیاری از ابعاد سیستم بدون تکنیک مدل‌سازی امکان پیش‌برد کار وجود ندارد.

مثال: دو تاس را با هم پرتاب می‌کنیم و متغیر تصادفی X را برابر مجموع اعداد روی دو تاس مشاهده شده در نظر می‌گیریم.

• تابع احتمال X را بدست آورید.
• احتمال اینکه مجموع اعداد روی دو تاس حداکثر 4 شود را بیابید.
• احتمال اینکه مجموع اعداد روی دو تاس بین 6 و 9 شود را بیابید.

حل         

فضای نمونه جمع عدد دو تاس برابر می‌شود با: R = S_X = {2, 3,…, 12}. برای بدست آوردن تابع احتمال X برای تمامی X ها بگوییم P(X = 1,…,12) = ?. به عنوان مثال می‌توان گفت:

به تابع f_X(x)، تابع PMF (probability mass function) نیز گفته می‌شود.

با محاسبه احتمالات مربوط به مجموعه بهینه شده، تابع احتمال X به صورت زیر بدست می‌آید. در نظر داشته باشید جمع PMF های از 0 تا بی‌هایت 1 خواهد شد.

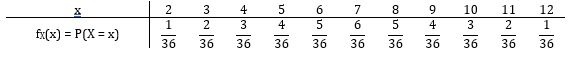
احتمال اینکه مجموع اعداد روی دو تاس حداکثر 4 شود برابر است با P(X <= 4) که برابر است با حالت‌های مجموع 2,3,4 و برابر است با مجموع توابع PMF آنها:

ت.

می‌توان به جای X هر عددی انتخاب کرد. اما اگر این اعداد در مجموعه R نباشد، تابع احتمال آن 0 خواهد شد.

تابع توزیع تجمعی

یکی از راه‌های توصیف توزیع متغیر‌های گسسته، استفاده از تابع جرم احتمال (PMF) است. به‌طور دقیق‌تر می‌توان گفت که تابع جرم احتمال را نمی‌توان برای متغیر‌های تصادفی پیوسته تعریف کرد و تابع توزیع تجمعی (CDF) مربوط به یک متغیر تصادفی، راه جایگزینی به‌منظور توصیف متغیر‌های تصادفی است.

مزیت تابع توزیع تجمعی این است که می‌توان آن را برای هر نوع از متغیر تصادفی تعریف کرد. تابع توزیع تجمعی برای متغیر تصادفی X، مطابق با گزاره زیر تعریف می‌شود.

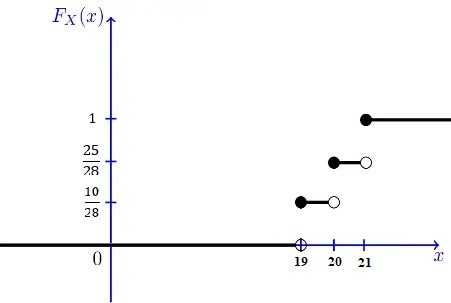
مثال: یک کلاس آمار 8 شاگرد دارد که 5 نفر آنها 19 ساله و 3 نفر آنها 21 ساله هستند. از این کلاس 2 شاگرد به تصادف و بدون جایگذاری انتخاب می‌کنیم و متغیر تصادفی X را برابر میانگین سن 2 شاگرد انتخابی در نظر می‌گیریم. تابع احتمال و تابع توزیع متغیر تصادفی X را به دست آورده و P(19 <X<21) را محاسبه کنید.

حل        در ابتدا S_X را بدست می‌آوریم. با توجه به اینکه سن شاگردان 19، 20 و  21 است، میانگین سنی برحسب اعداد طبیعی آنها یا 19 یا 20 و یا 21 خواهد بود. بنابراین S_X = {19, 20, 21}.

تابع احتمال به ازای فضای بهینه شده برابر است با

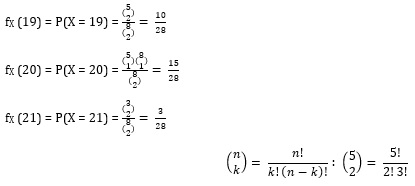
بنابراین تابع احتمال X برابر است با

تابع توزیع X به صورت زیر بدست می‌آید

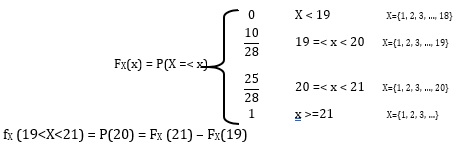
در نظر داشته باشید، همیشه تابع CDF به صورت تجمیعی است و پلکانی افزایش می‌یابد.