پیش نیاز بخش سه آمار و احتمال در ارزیابی کارایی سیستم، بخشهای مقدماتی و بخش دو است.
متغیرهای تصادفی گسسته رایج
برخی از انواع متغیرهای تصادفی گسسته شامل،: Constant، Uniform، Bernoulli، Binomial، دو جملهای منفی، Geometric و Poisson میباشد. متغیر تصادفی poisson خیلی در مدلسازی سیستمهای کامپیوتری کاربرد دارد که آن را بررسی خواهیم کرد.
اگر پدیدهای در دنیای کامپیوتر وجود داشته باشد که بتوان به یکی از مفاهیم متغیرهای تصادفی انطباق داد، میتوان از روابط آن متغیر تصادفی برای مدلسازی استفاده نمود.
تابع توزیع تصادفی ثابت – constant
برای یک عدد حقیقی c، تابع X به وسیله X(s) = c برای تمام sها در S تعریف میشود. در این حالت مشخصا P(X = c) = 1. در نتیجه توابع pmf و cdf این متغیر تصادفی برابر زیر است.
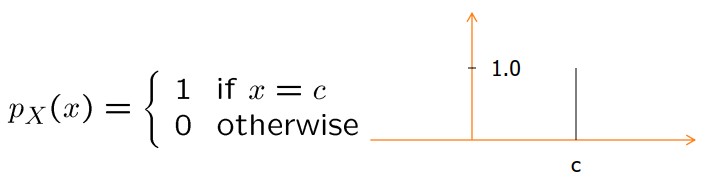
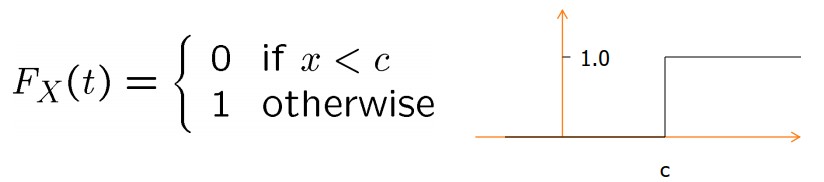
تابع توزیع یکنواخت گسسته – Uniform
در نظر بگیرید که X یک متغیر تصادفی با نگاشت متناهی {x1, x2, …, xn} است. یکی از سادهترین pmfهایی که در این حالت در نظر گرفته میشود این است که هر مقدار در نگاشت احتمال یکسانی دارد. اگر برای تمام iها، px(𝑥i) = p سپس
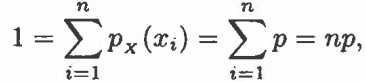
در نتیجه میتوان به معادله زیر رسید.
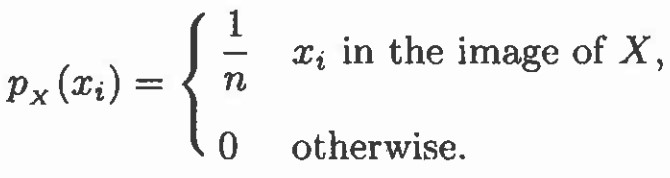
در این حالت گفته میشود که چنین متغیر تصادفی دارای توزیع یکنواخت گسسته است.
اگر X مقادیر {1, 2, …, n} با px(i) = 1/n که 1 ≤ i ≤ n، آنگاه تابع تجمیع توزیع آن برابر است با
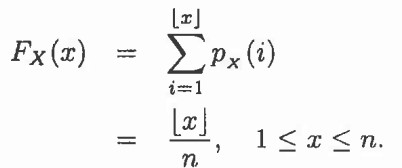
گراف این توزیع با n = 10 مانند تصویر زیر خواهد شد.
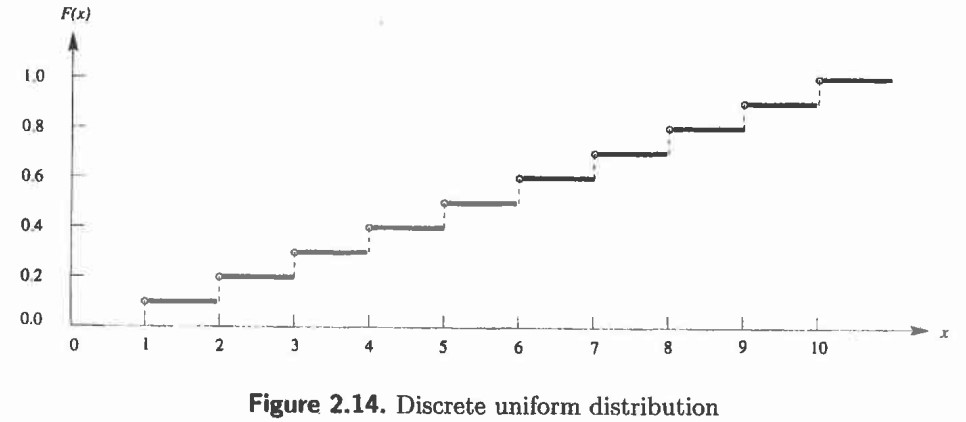
تابع توزیع برنولی – Bernoulli Trials
یک امتحان تصادفی را در نظر بگیرید که دو حالت خروجی ممکن به عنوان “موفقیت” و “شکست” دارد. چنانچه حالتهای خروجی را به صورت p (موفقیت) و q (شکست) در نظر بگیریم، آنگاه p + q = 1 خواهد شد. حال آزمایش ترکیبی را در نظر بگیرید که متشکل از یک تکرار n تایی مستقل از هم (مانند پرتاب n بار سکه) باشد. این توالی به عنوان توالی آزمایشات برنولی (Bernoulli trails) شناخته میشود. این دنباله بسیاری از حالتهای واقعی را میتواند مدل کند. به عنوان مثال، n اجرای متوالی دستور if را در نظر بگیرید که در آن موفقیت با دستور then و شکست با دستور else اجرا میشود.
اگر 0 مشخص کننده شکست و 1 مشخص کننده موفقیت باشد، Sn را به عنوان فضای نمونه یک آزمایش شامل n آزمایش برنولی در نظر میگیریم که به صورت زیر تعریف میشود.
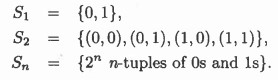
در این صورت احتمال در فضای نمونه S1 که قبلا نیز آن را مشخص کردیم، برابر با معادله زیر خواهد شد:
![]()
حال میخواهیم، احتمالات را به نقاط فضای نمونه Sn نسبت یا نگاشت دهیم. برای این کار، اگر در فضای نمونه Sn، مقدار Ai را به عنوان موفقیت آزمایش i ام و Āi را به عنوان شکست آزمایش i ام در نظر بگیریم، P(Ai) = p و P(Āi) = q و s یک عنصر از Sn باشد به صورتیکه s = (1, 1, …, 1, 0, 0, …, 0) که شامل k عدد 1 و n-k عدد 0، در این حالت پیشامد ابتدایی {s} میتواند به صورت زیر نوشته شود.
![]()
و در صورت مستقل و یکسان احتمال تکرارها احتمال کل حالات آن برابر میشود با
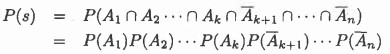
بخاطر مستقل بودن آزمایشات خواهیم داشت:
![]()
هر آزمایشی با تعداد کل n و تعداد k عدد 1 و n-k عدد 0 نیز همین نتیجه را خواهد داشت.
تابع توزیع دو جملهای – Binomial
تابع توزیع دو جملهای برابر است با تعداد k موفقیت در n آزمایش برنولی است. اگر فرمول بدست آمده در آزمایش برنولی را در نظر بگیریم که نتایج بدست آمده در حالتهای ثابتی بود، به همین ترتیب میتوان گفت، از آنجایی که به تعداد ![]() حالت میتوان آزمایشی مشابه آزمایش بالا انجام داد، پس میتوان گفت احتمال بدست آوردن k موفقیت در n آزمایش برابر معادله زیر خواهد شد:
حالت میتوان آزمایشی مشابه آزمایش بالا انجام داد، پس میتوان گفت احتمال بدست آوردن k موفقیت در n آزمایش برابر معادله زیر خواهد شد:
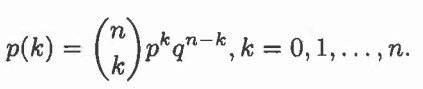
با توجه به فرمول بدست آمده میتوان گفت تابع cdf توزیع دو جملهای برابر است با:
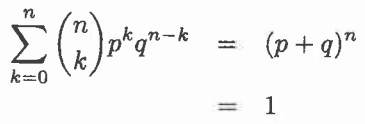
به عبارت دیگر در آزمایش دو جملهای میتوان گفت نگران توالی موفقیتها و شکستها نخواهیم بود و فقط بروی احتمال تعداد موفقیتها و شکستها توجه میکنیم.
مقادیر و نمودار تابع pmf توزیع دو جملهای اگر n = 10 و p = 0.75 باشد برابر با حالت زیر است.

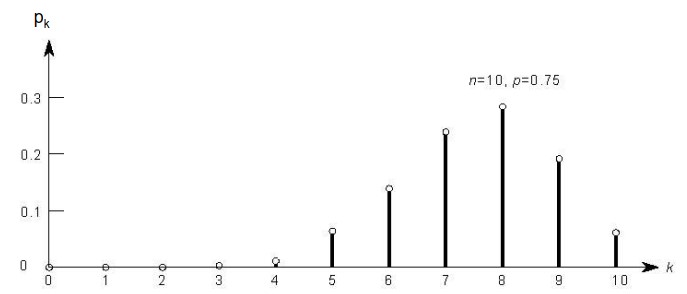
سیستم k-out-of-n
یکی از کاربردهای توزیع دو جملهای سیستم k-out-of-n است. برای اینکه سیستمی که از n زیرسیستم تشکیل شده کار کند بایستی حداقل k زیرسیستم کار کنند. به این سیستم، سیستم k-out-of-n گفته میشود.
در سیستمی با n زیرسیستم کاملا موازی حداقل باید یک زیرسیستم کار کند تا سیستم کار کند. در این حالت k برابر 1 خواهد بود.
در سیستمی با n زیرسیستم کاملا سری باید تمام زیرسیستمها کار کنند تا سیستم کار کند. در این حالت k برابر n خواهد بود.
برای مدل کردن reliability سیستم k-out-of-n میتوان از تابع توزیع دو جملهای استفاده کرد که در آن احتمال تعداد k موفقیت را میتوان بدست آورد. اگر فرض کنیم که تمام n زیرسیستم یکسان بوده (یعنی دارای reliabilityهای برابر هستند) و به صورت مستقل از هم کار میکنند و R را reliability یک زیرسیستم در نظر بگیریم (و q = 1 – R نمایش دهنده unreliability است) فرمول مدلسازی reliablity سیستم برابر میشود با:

از فرمول بدست آمده میتوان reliability سیستم سری و موازی که پیشتر بدست آورده بودیم را مجدد محاسبه کنیم بررسی کنیم که آیا نتیجه یکسان است یا خیر. در سیستم موازی k برابر 1 است. در نتیجه خواهیم داشت:
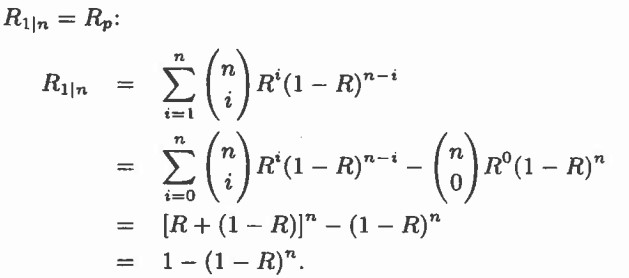
در محاسبات قبلی برای سیستمی با زیرسیستمهای کاملا موازی فرمول بدست آمده برابر بود با ![]() . اگر reliability هر زیر سیستم R شود نتیجه یکسان خواهد بود.
. اگر reliability هر زیر سیستم R شود نتیجه یکسان خواهد بود.
اگر زیرسیستمها کاملا سری باشند میتوان از فرمول سیستم k-out-of-n به فرمول سیستم سری رسید. در سیستم سری k برابر است با n
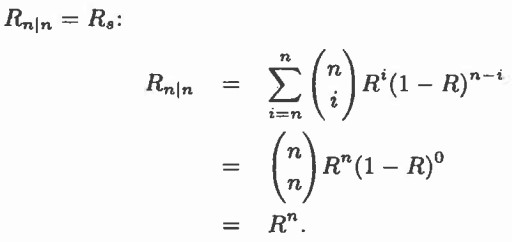
فرمول بدست آمده در محاسبات قبلی برابر است با: ![]() . در اینجا نیز اگر reliability هر زیر سیستم R شود نتیجه یکسان خواهد بود.
. در اینجا نیز اگر reliability هر زیر سیستم R شود نتیجه یکسان خواهد بود.
تابع توزیع متغیر تصادفی هندسی – Geometric
در تابع توزیع متغیر تصادفی هندسی، رسیدن به اولین موفقیت در آزمایشات برنولی مورد توجه است. به عبارت دیگر توزیع هندسی، توزیعی است گسسته که بیانگر احتمال اولین موفقیت پس از k-1 بار شکست در فرآیند برنولی باشد.
فرض کنید آزمایشهای مستقلی با احتمال موفقیت p آن قدر تکرار میشود تا یک موفقیت به دست آید. اگر X تعداد آزمایشهای لازم و احتمال آزمایشات برنولی برابر با فرمول زیر باشد:
![]()
از آنجایی که k به دلیل اینکه اولین موفقیت مورد نظر برابر 1 خواهد بود، آنگاه:
![]()
به این ترتیب تابع توزیع (جرم) تجمیع متغیر تصادفی هندسی برابر میشود با:
![]()
از مثالهایی از برنامهها و سیستمها منطبق با توزیع هندسی وجود دارد، تعداد دفعاتی که بخش شرطی حلقهها تکرار میشود تا نقض گردد.
while S do B
در آمار گفته میشود متغیر تصادفی هندسی خاصیت Memory-Less دارد. به این معنی که آنچه که در آینده اتفاق خواهد افتاد مستقل از اتفاقات گذشته است. منظور از مستقل بودن در نحوه وقوع پیشامدهای آینده است نه فرمول محاسبه. به همین ترتیب میتوان گفت اگر پیشامدی بیحافظه باشد یک توزیعی از نوع هندسی است.
مثال: فرض کنید احتمال قبولی یک نفر در امتحان رانندگی 0.7 باشد. احتمال اینکه این شخص در امتحان رانندگی:
الف) در مرتبه سوم
ب) حداکثر در سومین بار
قبول شود را بیابید.
حل:
الف) قبولی در مرتبه سوم بیانگر اولین قبولی در رخدادهای امتحان دادن است که پیشامد قبولی یا رد شدن دارد. با توجه در ملاک بودن اولین موفقیت، باید از طریق تابع متغیر تصادفی هندسی مساله را حل کنیم. برای قبولی در مرتبه سوم بایستی ممتحن دو بار اول را رد شود.
![]()
ب) زمانی که میگوییم حداکثر در سومین بار، بایستی در انتخاب X دقت کنیم.
![]()
تابع توزیع دو جملهای منفی – Negative Binomial
توزیع دو جملهای منفی یک توزیع احتمال گسسته است که تعداد موفقیتهایی را که در یک دنباله از آزمایشهای مستقل و با توزیع یکسان برنولی (با احتمال ثابت p) پس از تعداد مشخص و غیر تصادفی r شکست رخ میدهد را مدل میکند.
به عنوان مثال اگر آمدن عدد 6 در پرتاب یک تاس را به عنوان شکست و آمدن بقیه اعداد را بهعنوان موفقیت تعریف کنیم، میتوانیم بپرسیم قبل از اینکه سومین شکست (r = 3) را تجربه کنیم، چند پرتاب موفقیتآمیز رخ خواهد داد. در این حالت توزیع احتمال عدد غیر 6 (بقیه اعداد تاس) توزیع دو جملهای منفی خواهد بود. به طور مشابه میتوانیم از توزیع دو جملهای منفی برای مدل کردن تعداد روزهایی که یک دستگاه خاص قبل از اینکه خراب شود (r = 1) استفاده کنیم.
موفقیت و شکست الفاظی اختیاری هستند که میتوانند با هم جابجا شوند. از این رو میتوان گفت توزیع دو جملهای منفی توزیعی است از تعداد شکستها قبل از r موفقیت.
اگر X تعداد موفقیتها تا پایان آزمایش باشد، میتوان گفت توزیع این متغیر تصادفی با پارامترهای p و r است. آزمایش دوجملهای منفی، آزمایش دو جملهای تا r-1 است و حتما r امین آزمایش موفقیت است. در این حالت میتوان گفت، X دارای توزیع دو جملهای منفی با پارامترهای r و p است.
![]()
اگر X یک متغیر تصادفی با فضای نمونه اعداد صحیح مثبت باشد، توزیع احتمال r اُمین موفقیت در n آزمایش به شرطی که آخرین نتیجه آخرین آزمایش موفقیت باشد، به صورت است:
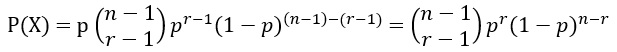
مثال: یک دانش آموزش برای گردش عملی تابستان احتیاج به پول دارد. او برای کسب درآمد تصمیم میگیرد تعدادی آبنبات به همسایگان بفروشد. در محله او 37 خانه وجود دارد. اگر او 5 آبنبات بفروشد، هزینه گردش عملی را تهیه کرده است. احتمال اینکه آخرین آبنبات لازم را در خانه 10ام بفروشد چقدر است.
احتمال خرید آبنبات در هر خانه ثابت و برابر 0.6 است.
حل: مساله برابر است با r موفقیت در n آزمایش به شرطی که آخرین آزمایش موفقیتآمیز باشد. به همین علت به سراغ توزیع دو جملهای منفی میرویم. در این مساله، فروش 5 آبنبات موفقیت است. تعداد آزمایشها نیز برابر است با n = k + 5 که تعداد خانههایی را نشان میدهد که دانش آموز باید برای فروش به آن ها مراجعه کند.
برای شروع محاسبه، ابتدا باید در n-1 آزمایش قبلی به r-1 موفقیت برسیم و نتیجه آزمایش nام هم موفقیتآمیز باشد.
![]()
مثال: فرض کنید 40 درصد از ماهیهای یک دریاچه از نوع بخصوصی باشند. اگر هر بار یک ماهی گرفته و نوع آن را مشخص کرده و دوباره به دریاچه بازگردانیم.
احتمال اینکه در دهمین بار، چهارمین ماهی از نوع فوق مشاهده شود را بیابید.
حل: در مسائل اگر بخواهیم به rاَمین موفقیت برسیم، باید مساله را از طریق دو جملهای منفی حل کنیم. دقت کنید که با برگرداندن ماهی به استخر، فضای نمونه نیز تغییر نمیکند. در این حالت X از نوع دو جملهای منفی با پارامترهای 4 و 0.4 است. ![]()
اگر بگوییم که در 10 امین بار 4 امین ماهی از نوع مورد نظر صید شود، به معنی این است که در 9 بار قبلی 3 بار این نوع ماهی صید شده و 10 امین بار دقیقا این ماهی صید شد. به این ترتیب احتمال آن برابر میشود با
![]()
تابع توزیع متغیر تصادفی پوآسون – Poisson
در آمار و احتمال، توزیع پوآسون یک توزیع احتمالی گسسته است که احتمال اینکه یک حادثه به تعداد مشخصی در فاصله زمانی یا مکانی ثابتی رخ دهد را شرح میدهد. آزمایش پوآسون باید دارای شرطهای زیر باشد.
- بین دو فاصله مجزای مکانی مانند (d1, d2) و (d3, d4) رخداد پیشامد مستقل از هم باشند. این قانون برای دو فاصله مجزای زمانی مانند (t1, t2) و (t3, t4) نیز وجود دارد.
- در هر فاصله زمانی یا مکانی کوچک، وقوع بیش از یک پیشامد صفر است.
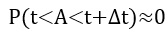
- احتمال رخداد یک پیشامد با طول فاصله مکانی یا زمانی متناسب باشد. به عنوان مثال، اگر طول یک فاصله مکانی برابر با d باشد، احتمال رخداد یک پیشامد در این فاصله برابر با λd باشد که در آن λ ضریب تناسب یک عدد حقیقی مثبت است.
همانطور که دیده شد، وقوع یا عدم وقوع یک پیشامد در این آزمایش ملاک است. پس میتوان نتایج آزمایش پوآسون را به شکلی با آزمایش و توزیع دو جملهای مرتبط دانست.
تعداد قطعیها در ارسال پیامهای کامپیوتری در یک فاصله زمانی مثالی از فرآیند پوآسون است زیرا:
- پیشامد قطعی در میلی ثانیه اول از قطعی در میلی ثانیه دوم مستقل است.
- در هر واحد کوچک زمانی احتمال قطع ارتباط بیش از یک بار تقریبا صفر است.
- تعداد قطعیها با طول زمان ارسال پیام بستگی دارد.
این محاسبات برای توصیف رفتار ورودی یک سیستم کمک خواهد کرد. میزان ورودی ترافیک به یک دستگاه در بازه 10 دقیقه – میزان درخواست خواندن از یک دیتابیس در باز 60 ثانیه – میزان FAIL کردن یک سیستم در یک سال – غیره
اگر تعداد موفقیتها (رخداد پیشامد مورد انتظار) k باشد، فرمول محاسبه تابع توزیع متغیر تصادفی پوآسون به شرح زیر است:
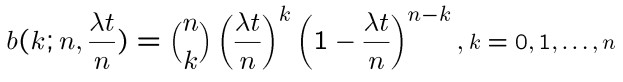
و اگر n به سمت بینهایت برود خواهیم داشت:
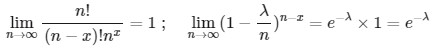
که باعث میشود فرمول به ابتدایی به حالت زیر تبدیل شود.
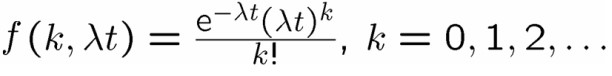
که λ برابر است با میانگین تعداد بستههای ورودی به دستگاه یا فراخوانی از دیتابیس در این بازه زمانی.
مثال: در یک کارخانه تولید خودرو، احتمال اینکه خودرو به دلیل نقص فنی در قسمت کنترل کیفیت بازگشت داده شود برابر یک درصد است. احتمال آنکه در بین 300 دستگاه تولیدی 5 دستگاه برگشت داده شود چقدر است؟
حل: در این گونه مسائل، متوسط مطرح شده همان پارامتر توزیع پوآسون است. از متن سوال متوجه میشویم که متوسط خودروهای بازگشتی برابر یک درصد است که در بین 300 دستگاه معادل 3 دستگاه است. حال اگر بخواهیم احتمال بازگشت خوردن 5 دستگاه را بررسی کنیم میتوان از فرمول پوآسون نوشت:
![]()
مثال: یک کارگزار بیمه به صورت متوسط در هفته سه قرارداد بیمه با مشتری امضا میکند. احتمال اینکه در طول یک هفته حداقل یک بیمه نامه بفروشد چقدر است؟
حل: از آنجایی که در هر واحد زمان نباید بیش از یک بیمه نامه فروخته شود (حداقل یک بیمه نامه) کافی است تا تعداد فروش بیمه نامه متناسب با زمان در نظر گرفته شود تا شرایط آزمایش پوآسون محقق شود.

مثال: یک دستگاه چاپگر کامپیوتری به طور متوسط در هر ماه 2 بار سرویس میشود.
الف) احتمال اینکه در یک ماه کمتر از 2 بار سرویس شود
ب) احتمال اینکه در سه ماه این چاپگر حداقل 2 بار سرویس شود
را بیابید.
حل:
الف) میانگین خرابی برابر است با 2 که همان مقدار λ است.
![]()
ب) از آنجایی که در این قسمت در صورت مساله زمان تغییر کرده است، به همین خاطر بایستی میزان میانگین را تطبیق دهیم که به عدد 6 تغییر میکند.
![]()
مثال: به طور متوسط هر ده دقیقه 6 مشتری به پای صندوق پرداخت یک فروشگاه میرسند. احتمال اینکه
الف) در 10 دقیقه حداکثر 4 مشتری
ب) در 5 دقیقه حداقل 2 مشتری
به پای صندوق برسند را بیابید.
حل:
الف) میانگین در این قسمت برابر است با 6.
![]()
ب) میانگین در این قسمت برابر است با 3.
![]()
متغیرهای تصادفی توام – Joint
ترکیب متغیرهای تصادفی مانند جمع، ضرب، کمینه، بیشنه، اشتراک، اجتماع و … یک متغیر تصادفی جدید ایجاد خواهد کرد.
مثال: از داخل جعبهای که شامل 3 توپ آبی، 2 توپ قرمز و 4 توپ سبز است، 2 توپ به تصادف یک به یک و بدون جایگذاری انتخاب میکنیم. اگر
X = تعداد توپهای آبی مشاهده شده در 2 توپ انتخابی
Y = تعداد توپهای قرمز مشاهده شده در 2 توپ انتخابی باشد،
الف) تابع احتمال توام (X, Y) را بدست آورید.
ب) P(X + Y ≤ 1) را محاسبه کنید.
حل: ابتدا باید برای X و Y فضای نمونه ایجاد کنیم که برابر است با SX = SY = {0, 1, 2}. سپس باید تمامی حالتهای ممکن خارج کردن توپها را محاسبه کنیم. برای این کار بایستی جدول زیر تکمیل شود.

توجه داشته باشید که fX, Y(0, 0) به معنی احتمال این است که در 2 توپ انتخابی، 0 توپ آبی و 0 توپ قرمز (هر دو توپ سبز) باشد.
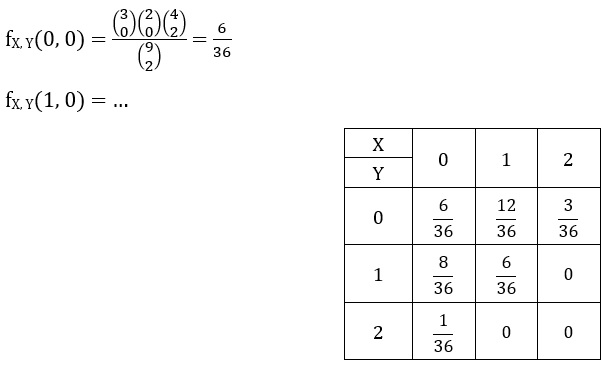
ب) از جدول بدست آمده میتوان این بخش را حل نمود. باید X + Y ≤ 1. در این حالت مقدار بدست آمده برابر است با