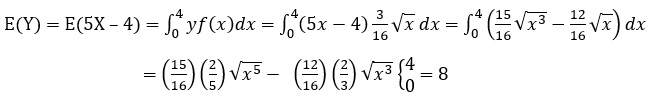پیش نیاز بخش چهار آمار و احتمال در ارزیابی کارایی سیستم، بخشهای مقدماتی، بخش دو و بخش سه است.
متغیر تصادفی پیوسته – Continues Random Variable
متغیرهای تصادفی پیوسته نوعی از متغیرهای تصادفی با خاصیتهای مشابه متغیر تصادفی گسسته هستند. تفاوت این دو متغیر با یکدیگر در فضای نمونه است. اگر فضای نمونه متغیر تصادفی X یک مجموعه نامتناهی غیرشمارا (Infinite – Uncontable) باشد، آن را یک متغیر تصادفی پیوسته مینامند. متغیرهای تصادفی پیوسته میتوانند تعداد نامحدودی از مقادیر ممکن را در یک محدوده یا بازه مشخص بگیرند.
تابع توزیع متغیر تصادفی پیوسته به شرح زیر میباشد:
![]()
اگر FX(x) یک تابع پیوسته از x باشد، آنگاه X یک متغیر تصادفی پیوسته است. در این حالت x میتواند از -∞ تا +∞ باشد و تابع FX(x) بین 0 و 1 خواهد بود.
![]()
اگر X یک متغیر تصادفی با تابع توزیع احتمال پیوسته FX باشد، آنگاه تابعی مانند fx وجود دارد که:
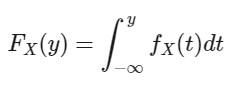
در این حالت fx را تابع چگالی (pdf) احتمال متغیر تصادفی X نامیده و میتوان نوشت:
![]()
برای محاسبه احتمال به کمک تابع چگالی (fX(y)) متغیر تصادفی X میتوان رابطه زیر را محاسبه کرد:
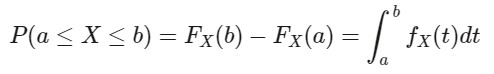
به عبارت دیگر و با توجه به مفهوم انتگرال، این احتمال برابر با سطح زیر منحنی تابع چگالی در بازه (a,b) میباشد.
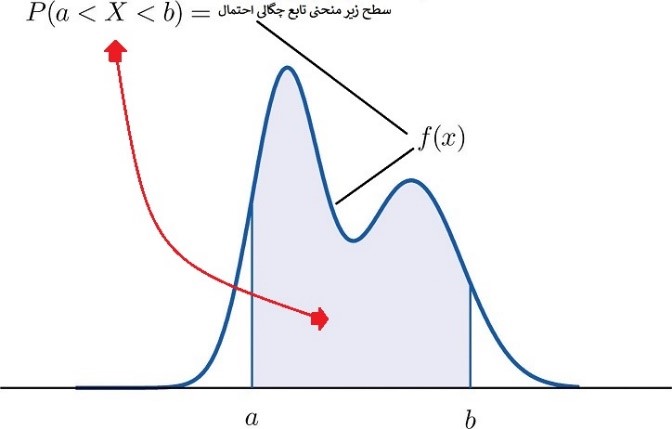
از آنجایی که نقطه سحطی از زیر نمودار را اشغال نمیکند پس میتوان گفت:
![]()
به همین علت میتوان علامت < را با ≥ و > را با ≤ عوض کرد.
در تابع توزیع پیوسته به جای تابع جرم احتمال (pmf)، تابع توزیع احتمال (PDF: Probability Distribution Function) داریم. در هر دو متغیر تابع تجمعی cdf نام دارد که در حالت گسسته سیگما و در حالت پیوسته انتگرال توابع pmf و PDF است.
همانند متغیرهای تصادفی گسسته، جمع تمامی احتمالات (تابع چگالی احتمال یا cdf) در متغیرهای تصادفی پیوسته نیز برابر 1 است.
![]()
با توجه به اینکه برای محاسبه احتمال نیاز به انتگرال گیری داریم. در این قسمت مقداری به یادآوری نحوه مشتق و انتگرال گیری میپردازیم.
مشتق
مفهوم مشتق در ریاضیات بیان میکند که یک پارامتر با چه سرعتی در زمان تغییر میکند. در حالت کلی مشتق بر دو نوع مشتق ساده و جزئی است. مشتقات ساده را میتوان با دو روش صریح و ضمنی بدست آورد.
فرض کنید میخواهیم شیب نمودار را در نقطه (x0,y0) بیابیم. برای این کار به نقطه دومی هم نیاز داریم. اگر این نقطه را به فاصله زیادی از (x0,y0) در نظر بگیریم، شیب بین این دو نقطه، عدد دقیقی از شیب در نقطه (x0,y0) نخواهد بود.
![]()
هر چقدر نقطه دوم نزدیکتر به نقطه اول باشد، مقدار به دست آمده دقیقتر خواهد بود.
![]()
به عبارت دیگر شیب نمودار همان مشتق تابع y نسبت به x یا به عبارت دیگر مشتق گیری y نسبت به x است. با این تعاریف میتوان گفت مشتق تابع y = f(x) نسبت به x برابر است با:
![]()
مثال: مشتق تابع f(x) = x را بدست آورید.
حل:
![]()
دیگر توابع معروف مشتق گیری شده
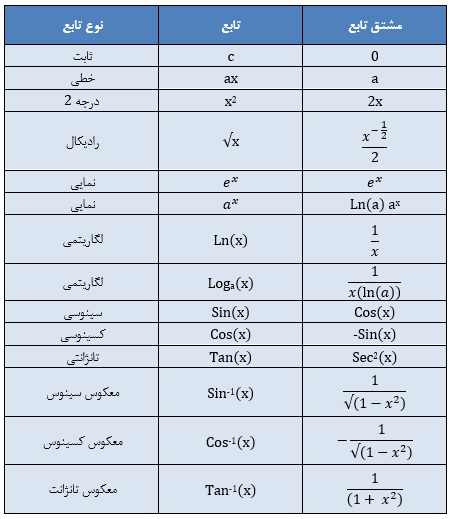
با استفاده از مشتقات توابع معرفی شده در بالا و قوانین حاکم بر مشتق میتوان مشتق هر نوع تابعی را بدست آورد.
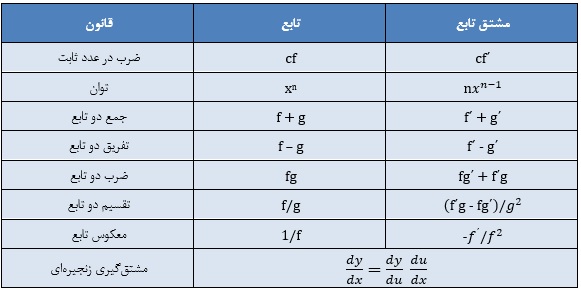
انتگرال
نماد استفاده شده برای توصیف انتگرال، s کشیده است. این حرف مخفف کلمه لاتین «Sum» به معنای جمع است. برای شروع، با استفاده از مساحت سطح زیر نمودار، به معرفی این مفهوم میپردازیم. بهمنظور درک مفهوم انتگرال در ابتدا بایستی با مشتق آشنایی داشته باشید.
با محاسبه مساحت بینهایت مستطیل بسیار کوچک در زیر نمودار، میتوان مقدار بسیار نزدیکی به اندازه سطح زیر یک نمودار را بدست آورد.
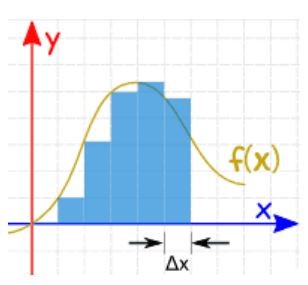
اما واقعا نیازی نیست برای محاسبه مساحت زیر نموارد مساحت تمام مستطیلها زیر آن را محاسبه کنیم تا تازه به یک مقدار تقریبی برسیم. نیوتن راه کوتاهتری را به ما نشان داده. او اثبات کرده که انتگرال و مشتق عکس هم هستند.
به عنوان مثال اگر بخواهیم انتگرال تابع y = 2x را بدست بیاوریم، از آنجایی که میدانیم مشتق تابع x2 برابر 2x است، بنابراین انتگرال 2x برابر است با x2.
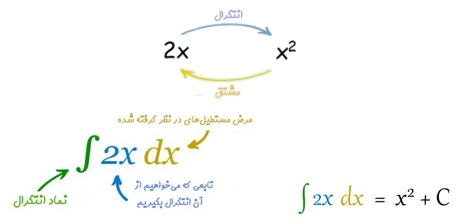
عدد C ثابت انتگرال است. دلیل قرار گرفتن C این است که اگر تابع x2 را با هر عدد ثابتی جمع کنیم و سپس از آن مشتق بگیریم، همچنان 2x ظاهر میشود.
مثال: فرض کنید متغیر تصادفی X دارای تابع چگالی احتمال زیر باشد.
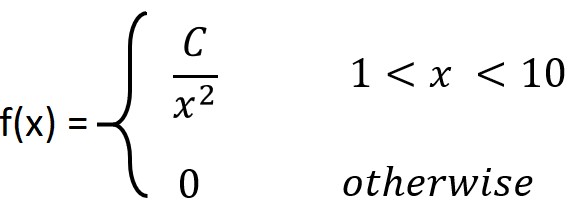
الف– مقدار C را تعیین کنید.
ب– تابع توزیع X را بدست آورید.
ج– احتمالات زیر را محاسبه کنید.
P(X > 2), P(1 < X ≤ 5), P([X] = 3)
حل:
الف– با توجه به تابع خواص چگالی احتمال (cdf) میتوان نوشت:
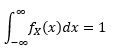
از آنجایی که تابع فقط بین اعداد 1 و 10 مقدار غیر صفر دارد، میتوان انتگرال را به سه قسمت زیر تبدیل کرد.
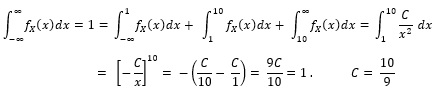
ب– برای بدست آوردن تابع توزیع بایستی FX(x) که انتگرال تابع fX(t) داده شده است را در سه بازه تا 1، از 1 تا x و از x را محاسبه کنیم.
با توجه به تابع چگالی احتمال داده شده،
برای x < 1 و x>=10 خواهیم داشت FX(t) = 0 که میتوان از آن صرف نظر نمود. به همین دلیل میتوان نوشت:
![]()
برای ![]() خواهیم داشت:
خواهیم داشت:
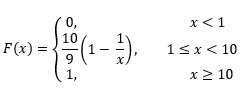
ج– به کمک انتگرال از تابع چگالی بدست آمده در قسمت الف و یا تابع توزیع قسمت ب میتوان احتمالهای مورد توجه قسمت ج را پاسخ داد.
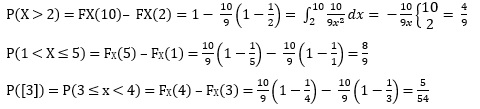
متغیر تصادفی و توزیع نمایی – Exponential
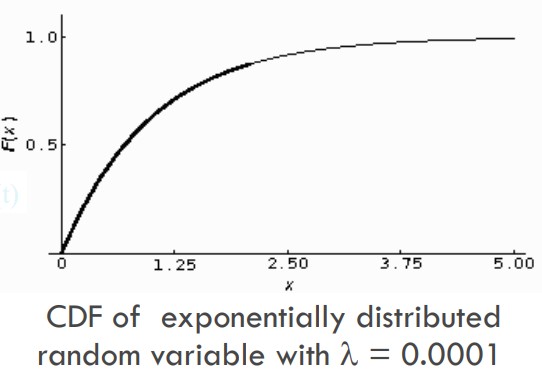
در آزمایش تصادفی پواسون، متغیر تصادفی تعداد رخداد در واحد زمان یا مکان بود. یکی از مهمترین بحثها در ارزیابی، مدلسازی ورودی یا workload سیستم است. مدلسازی تعداد ورودیها در یک بازه زمانی از طریق متغیر تصادفی و توزیع پواسون انجام میدهیم. یکی از پارامترهای مهم توزیع پواسون 𝜆 یا میانگین یا متوسط رخدادها (تعداد ورودیها) در یک بازه زمانی است.
حال اگر متغیر تصادفی را به زمان رسیدن به اولین رخداد یا زمان بین دو رخداد (مانند ورود دو بسته به دستگاه، دو فراخوانی یک تابع، دو درخواست به دیتابیس و …) تغییر دهیم، یک متغیر تصادفی پیوسته ایجاد شده که دارای توزیع نمایی است. بیشتر قطعات الکتریکی و الکترونیکی دارای طول عمری (زمان طی شده تا سوختن قطعه) با توزیع نمایی هستند که میتوان به کمک این توزیع احتمالهای مانند خرابی را تعیین کرد.
با این تعریف میتوان گفت متغیر تصادفی پواسون از جنس تعداد و متغیر تصافدی نمایی از جنس زمان است.
این تابع مانند تابع هندسی گسسته خاصیت بی حافظگی (Memoryless – رخدادهای آینده ربطی به گذشته ندارد) دارد. در این حالت میتوان گفت: اگر یک متغیر تصادفی پیوسته به همراه خاصیت بی حافظگی وجود داشت، تابع توزیعاش نمایی است.
مشخصه اصلی تابع نمایی رشد بسیار سریع آن است.
اگر X یک متغیر تصادفی پیوسته، با فضای نمونه نامتناهی اعداد حقیقی نامنفی باشد و تابع چگالی آن به صورت زیر نوشته شود، دارای توزیع نمایی است:
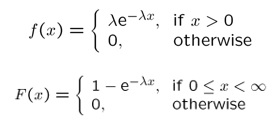
در این صورت X دارای توزیع نمایی با پارامتر 𝜆 خواهد بود که به صورت X ~ E(𝜆) نمایش داده میشود.
در این صورت برای رسیدن به متغیر تصادفی نمایی بایستی زمان رسیدن به اولین رخداد برابر با![]() باشد. معمولا متوسط زمان بین دو رخداد در توزیع نمایی با 𝜃 نمایش داده میشود. اگر بخواهیم فرمول را با متغیر 𝜃 بازنویسی کنیم میتوان گفت:
باشد. معمولا متوسط زمان بین دو رخداد در توزیع نمایی با 𝜃 نمایش داده میشود. اگر بخواهیم فرمول را با متغیر 𝜃 بازنویسی کنیم میتوان گفت:
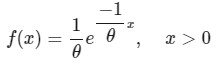
به یاد داشته باشید، اگر در مسالهای میانگین بازه زمانی به عنوان اطلاعات داده شد، آن را بایستی در محاسبات به صورت![]() بنویسیم.
بنویسیم.
مثال: طول عمر هر دستگاه کامپیوتر دارای توزیع نمایی با میانگین 1700 ساعت است. اگر آزمایشگاهی 20 دستگاه کامپیوتر داشته باشد، احتمال اینکه حداقل دو دستگاه از آنها قبل از 1700 ساعت خراب شود را بیابید.
حل:
متوسط ساعت اعلام شده به دلیل پیوسته بودن برابر با متغیر تصادفی پیوسته است و هر رخداد فارغ از رخداد دیگر اتفاق خواهد افتاد. به همین دلیل میتوان از تابع نمایی استفاده کرد.
X = طول عمر یک دستگاه کامپیوتر بر حسب ساعت
Y = تعداد دستگاههای کامپیوتر در بین 20 دستگاه که دارای طول عمر کمتر از 1700 ساعت هستند
X ~ E(1700) Y ~ B(20, p)
که در آن p احتمال خراب شدن یک دستگاه قبل از 1700 ساعت است و مقدارش براساس تابع چگالی قابل محاسبه است.
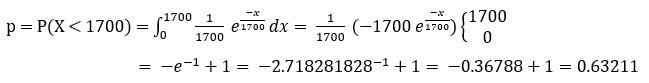
با بدست آمدن احتمال خرابی، حال میتوان از طریق تابع دو جملهای متغیر تصادفی گسسته (رسیدن به 2 موفقیت که در اینجا خرابی 2 دستگاه است مساله را حل نمود:
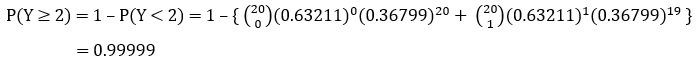
رابطه تابع توزیع نمایی و پواسون
آزمایش پواسون یک مدل برای توزیع تعداد اتفاقات (موفقیتها، شکستها، ورودیها، درخواستها، خرابیها) در یک زمان معین میباشد. به همین دلیل تعداد اتفاقات گسسته در یک بازه زمانی مشخص از مدل پواسون طبیعت میکند. زمان طی شده تا اولین اتفاق یا زمان طی شده بین دو اتفاق متوالی از یک توزیع نمایی پیروی میکند. به همین علت میتوان گفت در یک آزمایش که به زمان و تعداد دفعات تکرار یک رخداد وابسته است، توزیعهای نمایی و پواسون با یکدیگر در ارتباط خواهند بود.
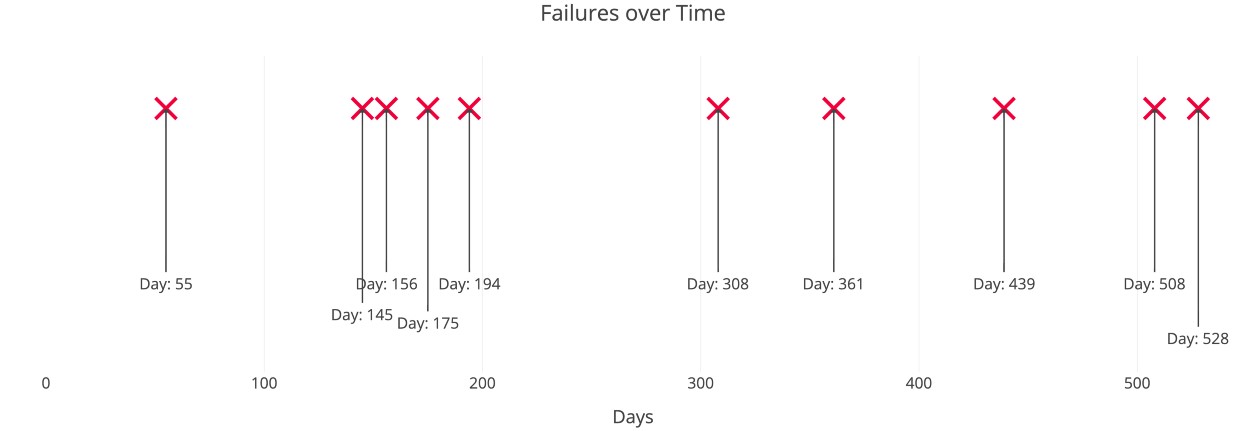
میتوان موضوع تشریح شده بالا را با فرمولهای احتمال به شرح زیر اثبات کرد (که البته نیازی به اثبات در ارزیابی کارایی نداریم):
در آزمایش پواسون پارامتر 𝜇 (میو) برابر است با میانگین تعداد اتفاقات در یک واحد زمانی، X، تعداد اتفاقات رخداده در فاصله زمانی [0,t] (پواسون) و Y زمان رسیدن تا اولین اتفاق (نمایی) میباشد.
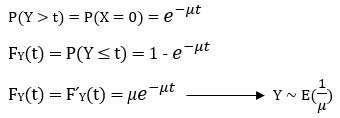
در آزمایش پواسون با پارامتر میانگین 𝜇، زمان رسیدن به اولین اتفاق دارای توزیع نمایی با عبارت![]() است، به عبارت دیگر Y یک توزیع نمایی با میانگین
است، به عبارت دیگر Y یک توزیع نمایی با میانگین![]() است. این مورد پیشتر به عنوان یادآوری نیز بیان شده بود.
است. این مورد پیشتر به عنوان یادآوری نیز بیان شده بود.
برای سادهتر شدن موضوع فرض کنید به یک سیستم کامپیوتری در هر یک ساعت به طور میانگین 10 پکت وارد میشود. فاصله زمانی تا ورود اولین پکت یا بین پکتها به صورت میانگین برابر است با 6 دقیقه. در این صورت، اگر پارامتر میانگین متغیر تصادفی پواسون برابر با 10 باشد، پارامتر میانگین توزیع نمایی برابر خواهد بود با ![]() .
.
مثال: به طور متوسط تعداد 5 تلفن در یک ساعت به تلفنخانه یک شرکت زده (تعداد 5 پکت به یک روتر در 1 ثانیه وارد) میشود.
الف- احتمال اینکه در یک ساعت حداقل 2 تلفن زده شود را بیابید.
ب- احتمال اینکه تلفن بعدی لااقل بعد از 15 دقیقه زده شود را بیاید.
ج- احتمال اینکه تلفن بعدی قبل از 10 دقیقه زده شود را بیابید.
حل:
به طور متوسط تعداد 5 تلفن (پارامتر میانگین پواسون)
پارامتر میانگین نمایی = 1/5
الف- زمانی که صحبت از تعداد (2 تلفن در یک ساعت) میشود باید به سراغ پواسون برویم. مرتبه پواسون نیز مشخص شده است که 5 است.
اگر X تعداد تلفنهایی باشد که در یک ساعت به شرکت زده میشود، آنگاه:
(در فرمول زیر λt همان میانگین رخداد پواسون در واحد زمان است)
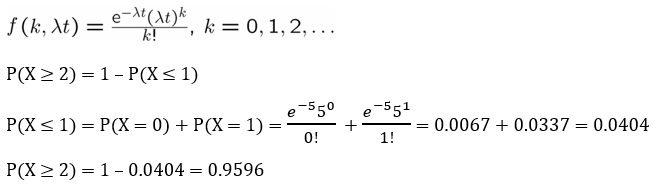
ب- زمانی که صحبت از “حداقل بعد از 15 دقیقه تلفن بعدی زده شود (اولین رخداد)” میشود، بایستی به سراغ توزیع نمایی برویم. باید توجه داشت که زمان مطرح شده در مساله به صورت میانگین هر 60 دقیقه بود، در حالیکه در قسمت ب، زمان را تغییر دادهایم. در این صورت خواهیم داشت:
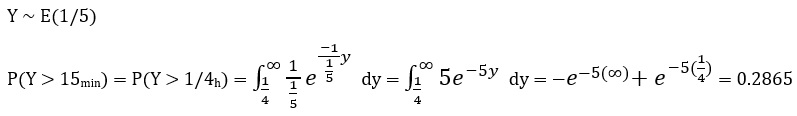
ج- حالت این بخش نیز مانند بخش قبلی است و از توزیع نمایی بایستی حل شود.
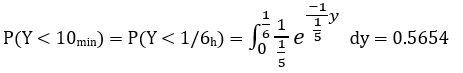
توزیع HypoExponential
هر سیستمی دارای زیرسیستمهای متنوعی مانند CPU، RAM، HDD، NIC و … است. هر کدام از این زیرسیستمها قابلیت مطرح شده احتمالهایی از نوع متغیر نمایی خواهند بود. اینگونه موارد که احتمال رخدادهای سیستمی با زیرسیستمهای متنوع را به صورت چند ترکیبی از چند متغیر تصادفی نمایی در کنار یکدیگر بررسی میکند را مدل HypoEponential مینامند.
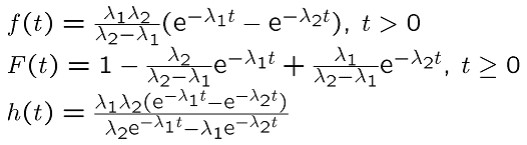
زمان سرویس یک هارد دیسک با HypoEponential مرتبه 3 مدل میشود که زمانهای آن به ترتیب برابر است با: زمان جستجو، زمان تاخیر و زمان انتقال.
توزیع Erlang
این توزیع حالت خاصی از HypoEponential است که پارامترهای همه مراحل یکسان است. توزیع Erlan یکی از توزیعهای مهم مورد استفاده از شیکههای مخابراتی است.
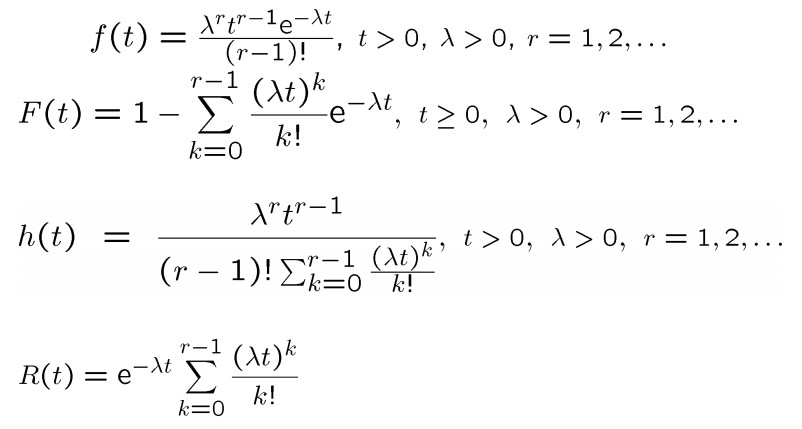
توزیع Gaussian (Normal)
این توزیع در حوزه مخابرات، تبعیت سینگال در ارسال اطلاعات بین دو نقطه، پیش بینیهای مواردی براساس سریهای زمانی استفاده مانند نرخ رشد اقتصادی، نرخ رشد یا کاهش بیکاری در 2 سال آینده، استفاده فراوان دارد. خیلی از پدیدههای فیزیکی نیز از مدل Gaussian یا ساده شده آن (Nromal) استفاده میکنند.
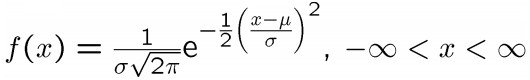
نرمال شده توزیع Gaussian برابر است با:
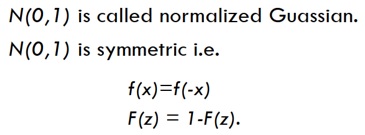
امید ریاضی – Expected (mean, average) value
ایده اصلی مطرح شده در مورد امید ریاضی به سالهای دور بر میگردد. زمانی که «بلز پاسکال» (Blaise Pascal) دانشمند و ریاضیدان فرانسوی در سال ۱۶۵۴ به مسئلهای با موضوع بازیهای شانسی برخورد کرد. او میخواست متوسط درآمد فردی که در چنین بازی شرکت میکند را محاسبه کرده و مشخص کند در صورتی که فرد در تعداد زیادی از این بازی شرکت کند آیا سود نصیبش خواهد شد و یا زیان هنگفتی خواهد کرد. او همچنین به میزان دارایی که بازیکن در هر مرحله صرف کرده توجه داشت و آن را به عنوان پارامتری در حل این مسئله در نظر گرفت.
فرض کنید فردی در یک بازی شانسی شرکت کرده است؛ احتمال برد او 0.2 است و در نتیجه احتمال اینکه ببازد نیز برابر با 0.8 است. همچنین فرض کنید که در صورت برنده شدن به وی مقدار 100 تومان داده میشود. ضمناً اگر بازی را ببازد، باید مبلغ 10 تومان جریمه پرداخت کند. به نظر شما او در این بازی نفع خواهد برد یا ضرر خواهد کرد؟
برای پاسخ به این سوال باید میانگین دریافت یا پرداختهای او را محاسبه کنیم.
از آنجایی که 0.2 احتمال دارد که 100 تومان برنده شود، اگر وارد بازی شود 20 تومان درآمد خواهد داشت. از طرفی ممکن است 8 تومان نیز جریمه شود. بنابراین به طور متوسط در هر بار بازی احتمال دارد 12 تومان درآمد کسب کند.
اگر X متغیر تصادفی باشد که فضای نمونه آن برابر با S = {x1, x2, …, xn} در نظر بگیریم و احتمال وقوع هر یک از مقدارهای فضای نمونه pi باشد، متوسط مقدر متغیر تصادفی X برابر خواهد بود با:
![]()
زمانی که متغیر تصادفی X پیوسته باشد، امید ریاضی به صورت انتگرال بدست میآید.
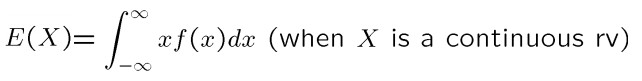
امید ریاضی از تابع توزیع نیز به صورت زیر قابل محاسبه است:
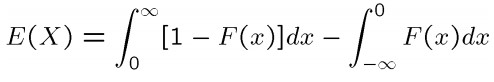
اگر X یک متغیر تصادفی گسسته با فضای نمونه S باشد، آنگاه امید ریاضی آن به صورت زیر تعریف میشود:
![]()
در این صورت امید ریاضی متغیر تصادفی برنولی برابر است با:
![]()
و امید ریاضی متغیر تصادفی هندسی برابر است با:
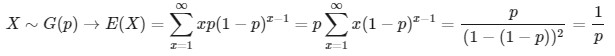
مثال: فرض کنید 40 درصد از ماهیهای یک دریاچه از نوع بخصوصی باشند. اگر هر بار یک ماهی گرفته و نوع آن را مشخص کرده و دوباره به دریاچه بازگردانیم.
انتظار میرود در چندمین صید ماهی، چهارمین ماهی از نوع فوق مشاهده شود؟
حل: وقتی در مسالهای میگوییم انتظار میرود به معنی امید ریاضی است.
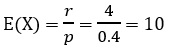
مثال: جعبهای شامل 2 مهره سفید و 3 مهره سیاه است. ابتدا یک مهره از این جعبه انتخاب میکنیم. متغیر تصادفی X را برابر تعداد مهرههای سفید در این یک مهره انتخاب شده در نظر میگیریم. سپس از مابقی مهرههای جعبه، دو مهره دیگر بدون جایگذاری انتخاب میکنیم. متغیر تصادفی Y را برابر تعداد مهرههای سفید مشاهده شده در این دو مهره انتخابی در نظر میگیریم.
تابع احتمال توام X و Y را به دست آورید.
E(X2, Y) را محاسبه کنید.
حل: در ابتدا بایستی فضای X و Y را بدست آوریم. در انتخاب اول، حالتهای سفید بوده مهره انتخابی برابر 0 و 1 است. در دو انتخاب دوم تمامی حالتهای موجود برابر است با 0، 1 و یا 2 مهره سفید.
SX = {0, 1} SY = {0, 1, 2}
برای بدست آوردن تابع توام X و Y باید تمامی حالتها (X,Y = 0,0 – 0,1 – …)در جدول متشکل از دو متغیر تصادفی برآورد شود.
اگر X=0 و Y=0 باشد به این معنی است که اولین و دومین مهره انتخاب هر دو سیاه باشند. باید در نظر داشته باشیم که پس از برداشتن مهره اول، فضای انتخابی مهره دوم یکی کم خواهد شد. احتمال انتخاب مهره اول انتخاب یکی از 3 مهره سیاه است که برابر میشود با 3/5.
در انتخاب 2 مهره دیگر، به دلیل اینکه همزمان دو مهره را برمیداریم، تعداد حالت کل یک انتخاب 2 مهره سیاه از 4 مهره و تعداد حالتهای برداشته 2 مهره سیاه از 2 مهره سیاه را حساب کنیم.
حالتهای دیگر را نیز به همین صورت حساب میکنیم.
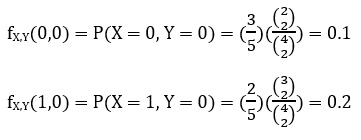
به همین ترتیب میتوان مقادیر دیگر را نیز حساب کرد که در جدول زیر قرار داده میشود.
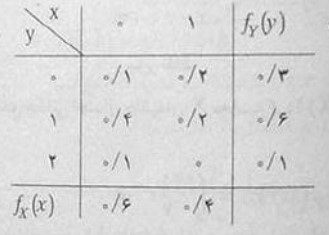
یادآوری: اگر![]() برای متغیرهای تصادفی گسسته یا
برای متغیرهای تصادفی گسسته یا![]() برای متغیرهای تصادفی پیوسته باشد، آنگاه
برای متغیرهای تصادفی پیوسته باشد، آنگاه
![]()
با توجه به گسسته بودن متغیرهای تصادفی این مساله برای محاسبه E(X2Y) میتوان نوشت
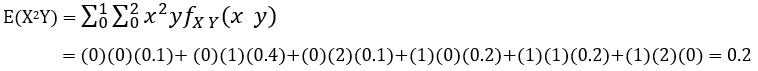
مثال: فرض کنید متغیر تصادفی X دارای تابع چگالی احتمال زیر باشد.
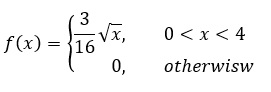
امید ریاضی Y = 5X – 4 را بدست آورید.
حل: باتوجه به اینکه مشخصا X یک متغیر تصادفی پیوسته است، بنابراین امید ریاضی آن برابر است با: